ページコンテンツ
リーマン予想の今を知ろう
数学の世界には超難問と呼ばれる中でもとびっきりの難しさと重要さを取り持つ「リーマン予想」。
19世紀にドイツ出身の数学者リーマンがだしたこの予想とついた難問は、素数の並びと、そこに潜む意味を解き明かすとされています。これまで多くの数学者たちが挑んできました。リーマン予想の完全な証明は今はまだいたっていませんが、現在はどこまで進んだのでしょうか。今回はリーマン予想についてのおすすめ書籍を紹介します。
ビジュアル リーマン予想入門 ~グラフで解き明かす素数とゼータ関数の関係
リーマン予想を視覚で理解する
「リーマン予想」とは、約1億円の賞金がかけられている数学界で最大の難問です。この予想で用いられる「ゼータ関数」は、「素数」と密接に関係しています。本書は、ビジュアルにこだわり視覚化したうえで、ゼータ関数と素数との関係を理解できるように解説しています。

はじめに
本書の目標
本書は,2016年に行った社会人,高校生・大学生向けセミナー「素数の世界~世紀の難問「リーマン予想とは!?」」(和から株式会社主催)の講義録を大幅に改訂したものです.私は,このセミナーの講師として,1回3時間全6回にわたり,数学を専門としない社会人・学生向けに,できるだけ分かりやすく数学の本質を見失わない程度に平易にしたうえでリーマン予想の解説を行いました.
「リーマン予想」とは,賞金100万ドル(約1億円)の懸賞金がかけられている数学界で最大の謎の一つです.ゼータ関数の零点に関する予想ですが,驚くべきことにこの「ゼータ関数」は,「素数」と密接に関係しているのです.同セミナーは,おかげさまでたくさんの方から応募があり好評をいただきました.一見素数とは何の関係もないように思われる「ゼータ関数」と「素数」が密接に関係しているということに,多くの方が「ロマン」を感じたのだと思います.私は当時もっていた知識を総動員して「ゼータ関数」と「素数」との関係を説明しましたが,セミナーが終了した後も,もっと分かりやすく「ゼータ関数」と「素数」との関係を説明できたらよいのにと常々思っていました.
本書の最終目標は,できるだけたくさんのグラフや図を利用して,この「ゼータ関数と素数との関係」を理解することにあります.この「素数」と「ゼータ関数(より正確にはゼータ関数の零点)」にはコインの「表」と「裏」のような関係があります.例えば,数が大きくなればなるほど素数の個数(出現割合)は減っていきますが,逆に,ゼータ関数の零点(零点の中でも非自明零点と言われるもの)は,数が大きくなればなるほど増えていきます.また,素数から得点を生成することも,逆に,零点から素数を生成することもできます.
本書の目標は,同セミナーでは十分に説明しきれなかった内容を含めて,ビジュアルに視覚化したうえで,この「素数とゼータ関数の零点との関係」を理解することにあります.
まずは,今後の見通しをよくするために,「素数」と「ゼータ関数」の関係をざっと見ていきましょう.この「はじめに」では,「ゼータ関数」や「零点」などの用語を詳しい説明をせずに使用していますが,詳細は後に説明しますので,ここでは分からなくても気にせず,「素数」と「ゼータ関数」の関係をざっと眺めてみてください.
素数
素数とは,2,3,5,7,11,13….など,1とその数以外に約数をもたない自然数です.Figure 1は,素数の位置に黒線を引いて素数の分布を表したものです.例えば,Figure 1(a)は,左端を1,右端を1000とし,一番左の黒線が2を,一番右側の黒線は997(1000以下の最大の素数)を表しています.1から1000までには素数が168個ありますので,168本の黒線が描かれています.バーコードみたいですね,名付けて「素数バーコード」です.同様に,(b)は1001から2000まで,(c)は100万1から100万1000まで,(d)は10億1から10億1000まで,(e)は1兆1から1兆1000までにある素数を黒線で表したものです.
これらを見ると,素数が現れる割合はどんどん減っていることが分かります.Table 1は,それぞれの開始数から1000個の自然数の中に何個の素数が含まれているか示したものです.素数の出現割合は減っていることが分かりますが,一方で「開始」が3桁(1000倍)増えているのに比べると,素数の出現割合はそれほど減っていないと捉えることもできます.「開始数」を1000倍したからといって,その周辺にある素数の数が1000分の1になるわけではないのです.このように,素数の出現割合は減っていくものの,その減り方はゆっくりなのです.この素数の出現割合がどのように減っていくのか表しているのが素数定理です.素数定理については,Part Iで詳しく見ていきます.
素数バーコードから分かることはこれだけではありません.素数バーコードを見ると,素数は満遍なく出現するのではなく,ところどころ偏りながら出現することも分かります,素数がしばらく現れない部分があるかと思えば,連続して素数が現れる部分もあります.この素数が現れる場所のことを素数の分布と言います.素数の分布を調べることとは,素数パーコードにおいて,黒線がどのような場所に現れるのか,また,どのような法則で現れるのかを研究することです.本書の最終目標は,この素数の分布がゼータ関数の零点でどのように表されるのか理解することにあります.
Table 1:自然数1000個当たりに含まれる素数の数と割合
| 開始数 | 素数の数 | 素数の割合 |
| 1 | 168 | 0.168 |
| 1,001 | 1351 | 0.135 |
| 1,000,001 | 75 | 0.075 |
| 1,000,000,001 | 49 | 0.049 |
| 1,000,000,000,001 | 37 | 0.037 |

ゼータ関数

Figure 2:ゼータ関数のグラフ
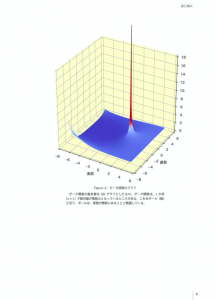
ゼータ関数の零点一自明な零点一

Figure 3: ゼータ関数の負のグラフ
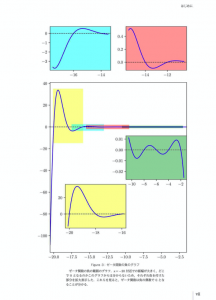
ゼータ関数の零点−非自明な零点−
ここまで,ゼータ関数のポールと自明な零点が素数の分布と関係があることをざっと見てきましたが,ゼータ関数には自明な零点の他に,もう一つの重要な得点の集まりがあります. Figure 4は,ゼータ関数の値(複素数)を偏角で色分けしたものです(偏角についてはPart III参照).このグラフからゼータ関数の零点を見つけていきましょう.上の図(a)は複素数の偏角を色分けしたカラーサンプルです.複素平面上で偏角が0(つまり実軸の正の方向)の付近は赤,半時計回りに黄色→緑となり,偏角が180度(つまり実軸の負の方向)では水色となって青→紫→赤に戻ってくることが分かります.原点は,赤・緑・青が接していることを覚えておきましょう.
下の図は,ゼータ関数の値の偏角をカラーで表したものです.右半平面(つまり,実部が正の範囲)上では赤一色になっています.これは,この範囲でゼータ関数の偏角が0付近にあることを示しています.また,負の実軸上では周期的に色が変わっているところがありますが,これが,先ほど見た自明な零点です.カラーマップで見たとおり赤・緑・青が接しているところが零点であり,例えばs= -2で赤・緑・青が接していることが分かります.同様に,負の偶数では赤・緑・青が接していることを確認できます,s=-2からs=-10までに赤・緑・青が接している部分が5個あることを確認してみましょう.
■非自明点
ゼータ関数の零点のうち,自明な零点以外を非自明な零点と言います.
Figure 4の下図では,赤・緑・青が接しているところがy軸上(つまり虚軸上)の付近にあることが分かります.例えば,虚軸の14の付近(つまり14i付近)に赤・緑・青が接しているところがあります.この点をよく見ると,虚軸からわずかに右側にずれていることが分かるでしょうか※2.21i,25i付近の虚軸からわずかに右側に外れたところにも,赤・緑・青が接している点があり,実は,ここにもゼータ関数の零点があるのです.これらが,ゼータ関数の非自明零点です.非自明零点については,Part VIIで確認します.
■リーマン予想
カラーマップを見ると,非自明零点は実軸からわずかに右側にずれた縦一直線にならんでいるように見えます.この縦の直線のことをクリティカルラインと言います.そして,本書のテーマであるリーマン予想とは,すべての非自明零点がクリティカルライン上にあるという予想です.コンピュータを使うことにより1兆個を超える非自明零点の位置が計算されていますが,現在までに判明している非自明零点はすべてクリティカルライン上にあります.つまり,現在までに判明している非自明零点は,すべてリーマン予想を満たしているのです.しかし,未だこの証明には誰も成功していません,リーマン予想についてはPart VIIで確認します.
※2 原点の右横にある赤・緑・青が接している部分は,点ではなくポールです.
Figure 4:ゼータ関数の偏角のカラーマッピング

非自明零点から素数を作る

Figure 5:非自明零点から素数の再現
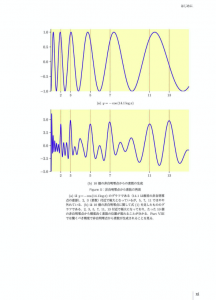
素数から非自明零点を作る

Figure 6:素数から非自明点の再現
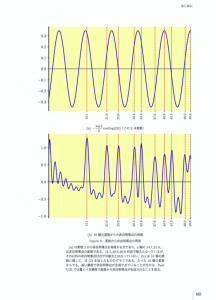
素数とゼータ関数のまとめ
ここまでお話ししてきた「ゼータ関数」と「素数」との関係はTable 2のとおりです.
ゼータ関数には,「ポール」と「零点」があり,「零点」には「自明な零点」と「非自明な零点」があります.このそれぞれが,素数との間で関係があるのです.
Table 2:ゼータ関数のポール・寄点と素との関係

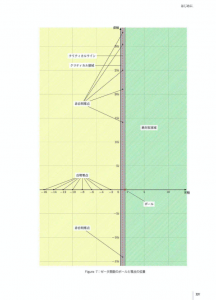
Figure 7: ゼータ関数のボールと書点の位置
Contents 目次
はじめに
Part I 素数の不思議な性質
第1章 素数の性質
1.1 素因数分解の一意性
1.2 素数が無限にあること
第2章 素数を数えよう
2.1素数を数える関数−素数計数関数π(x)−
2.2 素数計数関数の形状
2.3 素数定理入門
2.4 素数定理を精緻化する
Part II ゼータ関数
第3章 ゼータ関数登場
3.1 ゼータ関数
3.2 調和級数
3.3 調和級数による素数の無限性の証明
第4章 バーゼル問題 −ζ(2)の値−
4.1 バーゼル問題
4.2 sinxのテイラー展開
4.3 sinxの無限乗積展開
4.4 バーゼル問題を解く
4.5 ゼータ関数の正の偶数での値
4.6 ウォリスの公式
Part III imaginaryな世界へようこそ
第5章 複素数乗とは
5.1 定義域を複素数へ拡張する
5.2 複素平面
5.3 オイラーの公式
5.4 正の数の複素数乗
5.5 複素数の複素数乗
5.6 ゼータ関数の定義域を複素数へ拡張する
5.7 ゼータ関数の微分
第6章 正則関数の零点とポール
6.1 零点とポール(極)はなぜ重要か
6.2 正則関数の零点
6.3 正則関数のポール(極)
6.4 除去可能特異点
6.5 ローラン展開と留数
6.6 留数
6.7 留数定理
第7章 解析接続とは
7.1 ゼータ関数の定義域
7.2 関数の姿
7.3 解析接続とは
Part IV ゼータの兄弟−ガンマ関数−
第8章 ガンマ関数
8.1 階乗関数
8.2 ガンマ関数の定義
8.3 ガンマ関数の漸化式
8.4 ガンマ関数を解析接続する
第9章 ガンマ関数の性質
9.1 ガンマ関数の零点とポール
9.2 ガンマ関数の基本公式
Part V 1+2+3+…=-1/12
第10章 ゼータ関数の解析接続
10.1 一般二項定理
10.2 ゼータ関数の新化式
10.3 ゼータ関数の解析接続
第11章 ゼータ関数の整数での値−特殊値−
11.1 ゼータ関数のポール
11.2 Res<1における漸化式の簡易化
11.3 ζ(0)とζ(-1)を求める
11.4 ゼータ関数の解析接続−負の整数−
11.5 ベルヌーイ数とは
11.6 ゼータ関数の負の整数をベルヌーイ数で表す
第12章 オイラー,ラマヌジャンによる不思議な方法
12.1 1+2+3+4+…=-1/12?
12.2 オイラー,ラマヌジャンによる方法
12.3 片側極限
12.4 アーベル総和法
12.5 イータ関数
12.6 オイラー,ラマヌジャンの方法の正当化
12.7 ζ(0)を求める
Part VI 太陽と月の美しい関係
第13章 un beau rapport−オイラーによる美しい関係−
13.1 Beautiful Relation
13.2 オイラーによる関数等式
13.3 リーマンによる関数等式
第14章 関数等式の証明
14.1 ガンマ関数とゼータ関数の関係
14.2 関数等式(非対称型)から関数等式(対称型)の導出
14.3 関数等式の証明―積分を計算する―
14.4 関数等式の証明―もう一つの積分計算―
14.5 関数等式の証明―留数定理を用いる―
14.6 正の偶数における特殊値
Part VII リーマン予想
第15章 ゼータ関数の零点とリーマン予想
15.1 関数等式の意味
15.2 ゼータ関数の零点
15.3 リーマン予想
15.4 非自明零点の分布
第16章 リーマン予想と同値な命題
16.1 素数定理との関係
16.2 メビウス関数とメルテンス関数
16.3 メルテンス予想とリーマン予想
16.4 ファレイ数列
16.5 ファレイ数列とリーマン予想
Part VIII 素数で輝く
第17章 素数階段を表す
17.1 ゼータ関数と素数との関係
17.2 マンゴルト関数とチェピシェフ関数
17.3 ディリクレ級数と階段関数の関係―ペロンの公式―
17.4 ψ^xの積分表示
17.5 ψ^x(x)の明示公式
17.6 マンゴルト明示公式の意味―近似項―
第18章 素数定理
18.1 素数定理を用いて言い換える
18.2 補題18.1.1の証明
18.3 素数定理の証明のアイデア
18.4 Res=1上に零点がないこと
第19章 素数で輝く
19.1 リーマンスペクトル
19.2 マンゴルト明示公式の意味―周期項―
19.3 マンゴルトの明示公式のグラフ1
19.4 マンゴルトの明示公式のグラフ2
19.5 周期項を微分する
19.6 素数で輝く
19.7 リーマンスペクトルで輝く
リーマン予想の探求 ~ABCからZまで~ (知りたい! サイエンス)
リーマン予想を掘り下げる
リーマン予想は、数学最大の難問として有名です。本書では、リーマン予想に至る素数の研究を振り返り、リーマン予想の研究についてわかりやすく解説をします。また、21世紀のこれからは、全ての数学を行う「絶対数学」が重要になってくるということを踏まえて、絶対数学の導入にも役立つように書かれています。

はじめに
リーマン予想は数学最大の難問として有名です。その背景には今から2500年も昔のギリシャ時代からの素数の研究があります。現代の私たちにとっては、素数は小学校時代から接してきていて、簡単なものに思えてしまうかもしれません。しかし、素数という考えを最初に思いついた人の身になって、自分で発見することを想像してみると、並大抵なことではなかったことに気付きます。残念なことに、素数に思い至った偉大な数学者の名前は、知られていません。現在では、素数は数学研究だけでなく、物理学などでも活躍していますし、現代情報社会のセキュリティーの基盤を素数を用いた暗号として提供するという重要な役目も担っています。
本書では、リーマン予想に至る素数の研究を簡単に振り返り、リーマン予想の研究についてできるだけわかりやすく解説をしました。そこには、オイラー、リーマン、ラマヌジャン、コルンブルム、セルバーグといった素数とゼータ関数の研究において数学史に名前を残す人たちが登場します。彼らが、どのようにして研究を推進したかを体験してください。
リーマン予想は未解決問題ですし、これまでの研究は膨大なものです。そこで、本書の解説は筆者の考える重要と思われる視点と題材のみに限定してあります。21世紀のこれからは一元体からすべての数学を行うという「絶対数学」が、リーマン予想の研究だけに留まらず重要だと思います。本書は、絶対数学への導入も兼ねています。リーマン予想は新たな人々の挑戦をまっています。リーマン予想への航海に乗り出してください。
2012年9月18日
黒川信重
リーマン予想の探求 -ABCからZまで
Contents
序章 オイラーとリーマン
コラム ゼータ関数とリーマン予想の略年表
第1章 素数の歴史
ピタゴラスからオイラーまで
第2章 素数とリーマン予想の関係
コラム オイラーとリーマン
コラム ゼータは生き物である
第3章 オイラー積ふたたび
コラム オイラー全集
第4章 オイラー積を発見したラマヌジャン
第5章 コルンブルムとセルバーグ
コラム ゼータ正規化積
第6章 深リーマン予想
コラム ゼータはダイコン!?
第7章 リーマン予想の解読へ
付録 数論の有名な予想のいくつか
(1) abc予想
(2) 関数体版のabc予想の証明
(3) アルチンの原始根予想
(4) 関数体版のアルチンの原始根予想証明の歴史
(5) 一覧表
読書案内
索引
著者プロフィール
よく出てくる記号の読み方と意味

序章 オイラーとリーマン
素数の研究をしてきた人は、今から2500年くらい昔のギリシャ時代から、たくさんいました。その探求が現代のように深い研究になってきたのは、18世紀のオイラーさん(1707年-1783年)と19世紀のリーマンさん(1826年-1866年)のおかげです。それは、ゼータ(ζ)を使うという段階に至ったからです。
オイラーさんは素数2,3,5,7、…にわたる積(オイラー積)を考え、それが自然数1,2,3、…にわたる和に等しいことを見抜きました(1737年)。リーマンさんは、この関数をζ(s)と名付け、さらに、ζ(s)が0になる複素数(零点と呼びます)は実質的に実部が1/2という一直線上に乗っていると予想しました(すべての複素数sに対してζ(s)を意味づけることは複素関数論の解析接続という方法が必要になります)。これが、数学最大の難問と言われる『リーマン予想』です。このリーマン予想は1859年に提出されてから150年以上経ちましたが、未解決です。本書では、このリーマン予想とその一歩先を話したいと思います。
リーマンゼータ関数のはじめのほうの虚の零点は次のようになっています。
リーマンゼータ関数の虚の零点の例


このように、すべての虚の零点の実部が1/2である、というのがリーマン予想です。
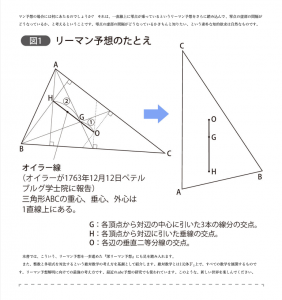
リーマン予想の感じをイメージしていただくために、素数やゼータとは離れた数学のところからの美しい定理を紹介しておきます。それは、オイラーさんが1763年12月12日にペテルブルグ(現在のサンクトペテルブルグ)学士院に報告した
『オイラー線定理:三角形の外心・重心・重心は一直線(オイラー線)上に乗っていて、間隔の比はこの順に1:2となる』
という不思議な定理です。リーマン予想の際の零点に外心・重心・垂心を対比して考え、一直線上に乗っているという同じ性質と眺めてもらえばよいのです。どんな三角形でも外心・重心・垂心は、なぜか、オイラー線というオイラー線という一直線上に乗っていて、ずれていないのです。しかも、間隔の比が1:1という等間隔ではなくて、なぜか1:2なのです。
リーマン予想は、この「一直線上に乗っている」という性質にあたります。では、オイラー線の場合に「間隔が1:2」という精密な性質は、リーマン予想の場合には何にあたるのでしょうか?それは、一直線上に零点が乗っているというリーマン予想をさらに踏み込んで、零点の虚部の間隔がどうなっているか、と考えるということです。零点の虚部の間隔がどうなっているかきちんと知りたい、という素朴な知的欲求は自然なものです。
図1 リーマン予想のたとえ

本書では、こういう、リーマン予想を一歩進めた『深リーマン予想』にも足を踏み入れます。
また、整数と多項式を対比するという絶対数学の考え方を基調として紹介します。絶対数学とは1元体F1上で、すべての数学を展開するものです。リーマン予想解明に向けての最強の考え方です。最近のabc予想の研究でも使われています。このような、新しい世界を楽しんでください。
コラム ゼータ関数とリーマン予想の略年表
1737年 オイラー:ゼータ(オイラー積)を発見し、素数とゼータが結びついた
1837年 ディリクレ:等差数列内の素数の分布をゼータを使って研究した
1859年 リーマン:ゼータの虚の零点を用いて素数分布公式を証明し、リーマン予想を提出した
1914年 ハーディ:リーマンゼータが実部1/2の零点を無限個持つことを証明した
1916年 ラマヌジャン:高次(2次)のゼータを発見し、ラマヌジャン予想を提出した
1919年 コルンブルム:合同ゼータを史上初めて発見[1914年没;遺稿がランダウにより出版]
1932年 ジーゲル:リーマンのゼータ研究遺稿を調査し報告[リーマン・ジーゲル公式の発見]
1933年 ハッセ:楕円曲線の合同ゼータに対するリーマン予想を証明した
1942年 セルバーグ:リーマンゼータの虚の零点のうち少なくとも正のパーセントは実部が1/2となることを証明した
1948年 ヴェイユ:代数曲線の合同ゼータに対するリーマン予想を証明した
1949年 ヴェイユ:合同ゼータ関数の一般的定式化(ヴェイユ予想)提出した
1952年 セルバーグ:セルバーグゼータ関数を発見し、リーマン予想の対応物を証明した
1962年、1963年 佐藤幹夫:ラマヌジャン予想を合同ゼータ関数に対するリーマン予想(ヴェイユ予想) に帰着させ、佐藤テイト予想を提出した
1965年 グロタンディーク:合同ゼータ関数の行列式表示を証明した[そのために一万ページに及ぶスキーム論EGA、SGAを構築]
1974年 ドリーニュ:合同ゼータ関数に対するリーマン予想(ヴェイユ予想)を証明した 1974年 レヴィンソン:リーマンゼータの虚の零点のうち少なくとも1/3(34パーセント)は
実部が1/2となることを証明した
1989年 コンリー:リーマンゼータの虚の零点のうち少なくとも2/5(40パーセント)は実部が1/2となることを証明した
1995年 ワイルズ(+テイラー):フェルマー予想を証明した(楕円曲線の標準ゼータによる)
2011年 テイラー達:佐藤テント予想を証明した(保型形式のゼータの無限系列を用いる)
20XX年 xxxx:リーマン予想解決
リーマン予想の今,そして解決への展望 (数学への招待)
リーマン予想の最新情報を知る
本書は、2012年刊行の知りたい!サイエンス『リーマン予想の探究〜ABCからZまで〜』に最新情報を加えつつ大幅に改定したものです。新しくリーマン予想へのキーワードと注目されてきた「黒川テンソル積」や「零和構造」も解説されています。

はじめに
リーマン予想は数学最大の難問として有名です。その背景には今から2500年も昔のギリシャ時代からの素数の研究があります。現代の私たちにとっては、素数は小学校時代から接してきていて、簡単なものに思えてしまうかもしれません。しかし、素数という考えを最初に思いついた人の身になって、自分で発見することを想像してみると、並大抵なことではなかったことに気付きます。残念なことに、素数に思い至った偉大な数学者の名前は、知られていません。現在では、素数は数学研究だけでなく、物理学などでも活躍していますし、現代情報社会のセキュリティーの基盤を素数を用いた暗号として提供するという重要な役目も担っています。
本書では、リーマン予想に至る素数の研究を簡単に振り返り、リーマン予想の研究についてできるだけわかりやすく解説をしました。そこには、オイラー、リーマン、ラマヌジャン、コルンブルム、セルバーグといった素数とゼータ関数の研究において数学史に名前を残す人たちが登場します。彼らが、どのようにして研究を推進したかを体験してください。
リーマン予想は未解決問題ですし、これまでの研究は膨大なものです。そこで、本書の解説は筆者の考える重要と思われる視点と題材のみに限定してあります。21世紀のこれからは一元体からすべての数学を行うという「絶対数学」が、リーマン予想の研究だけに留まらず重要だと思います。本書は、絶対数学への導入も兼ねています。リーマン予想は新たな人々の挑戦をまっています。リーマン予想への航海に乗り出してください。
2019年(平成31年)4月8日
黒川信重
リーマン予想の今、そして解決への展望
Contents
序章 オイラーとリーマン
コラム ゼータ関数とリーマン予想の略年表
第1章 素数の歴史
ピタゴラスからオイラーまで
第2章 素数とリーマン予想の関係
コラム オイラーとリーマン
コラム ゼータは生き物である
第3章 オイラー積ふたたび
コラム オイラー全集
第4章 オイラー積を発見したラマヌジャン
第5章 コルンブルムとセルバーグ
コラム ゼータ正規化積
第6章 深リーマン予想
第7章 リーマン予想の解読へ
コラム ゼータはダイコン!?
第8章 絶対数学の進展
付録 数論の有名な予想のいくつか
(1)abc予想
(2)関数体版のabc予想の証明
(3)アルチンの原始根予想
(4)関数体版のアルチンの原始根予想証明の歴史
(5)本書で扱った予想とロゼッタストーン(第2章「リーマン予想をロゼッタストーンになぞらえる」)の対応表
読書案内
索引
著者プロフィール
よく出てくる記号の読み方と意味

序章 オイラーとリーマン
素数の研究をしてきた人は、今から2500年くらい昔のギリシャ時代から、たくさんいました。その探求が現代のように深い研究になってきたのは、18世紀のオイラーさん(1707年-1783年)と19世紀のリーマンさん(1826年-1866年)のおかげです。それは、ゼータ(ζ)を使うという段階に至ったからです。
オイラーさんは素数2,3,5,7、…にわたる積(オイラー積)を考え、それが自然数1,2,3、…にわたる和に等しいことを見抜きました(1737年)。リーマンさんは、この関数をζ(s)と名付け、さらに、ζ(s)が0になる複素数(零点と呼びます)は実質的に実部が1/2という一直線上に乗っていると予想しました(すべての複素数sに対してζ(s)を意味づけることは複素関数論の解析接続という方法が必要になります)。これが、数学最大の難問と言われる「リーマン予想」です。このリーマン予想は1859年に提出されてから160年経ちましたが、未解決です。本書では、このリーマン予想とその一歩先を話したいと思います。
リーマンゼータ関数のはじめのほうの虚の零点は次のようになっています。
リーマンゼータ関数の虚の零点の例

このように、すべての屋の零点の実部が1/2である、というのがリーマン予想です。
リーマン予想の感じをイメージしていただくために、素数やゼータとは離れた数学のところからの美しい定理を紹介しておきます。それは、オイラーさんが1763年12月12日にペテルブルグ(現在のサンクトペテルブルグ)学士院に報告した
「オイラー線定理:三角形の外心・重心・重心は一直線(オイラー線)上に乗っていて、間隔の比はこの順に1:2となる」
という不思議な定理です。リーマン予想の際の零点に外心・重心・重心を対比して考え、一直線上に乗っているという同じ性質と眺めてもらえばよいのです。どんな三角形でも外心・重心・重心は、なぜか、オイラー線という一直線上に乗っていて、ずれていないのです。しかも、間隔の比が1:1という等間隔ではなくて、なぜか1:2なのです。
リーマン予想は、この「一直線上に乗っている」という性質にあたります。では、オイラー線の場合に「間隔が1:2」という精密な性質は、リーマン予想の場合には何にあたるのでしょうか?それは、一直線上に零点が乗っているというリーマン予想をさらに踏み込んで、零点の虚部の間隔がどうなっているか、と考えるということです。零点の虚部の間隔がどうなっているかきちんと知りたい、という素朴な知的欲求は自然なものです。
(図1) リーマン予想のたとえ
本書では、こういう、リーマン予想を一歩進めた「深リーマン予想」にも足を踏み入れます。
また、整数と多項式を対比するという絶対数学の考え方を基調として紹介します。絶対数学とは1元体F1上で、すべての数学を展開するものです。リーマン予想解明に向けての最強の考え方です。最近のabc予想の研究でも使われています。このような、新しい世界を楽しんでください。
コラム
ゼータ関数とリーマン予想の略年表
1737年 オイラー:ゼータ(オイラー積)を発見し、素数とゼータが結びついた
1837年 ディリクレ:等差数列内の素数の分布をゼータを使って研究した
1859年 リーマン:ゼータの虚の零点を用いて素数分布公式を証明し、リーマン予想を提出した
1914年 ハーディ:リーマンゼータが実部1/2の零点を無限個持つことを証明した
1916年 ラマヌジャン:高次(2次)のゼータを発見し、ラマヌジャン予想を提出した
1919年 コルンブルム:合同ゼータを史上初めて発見[1914年没;遺稿がランダウにより出版]
1932年 ジーベル:リーマンのゼータ研究遺稿を調査し報告[リーマン・ジーグル公式の発見]
1933年 ハッセ:楕円曲線の合同ゼータに対するリーマン予想を証明した
1942年 セルバーグ:リーマンゼータの店の零点のうち少なくとも正のパーセントは実部が1/2となることを証明した
1948年 ヴェイユ:代数曲線の合同ゼータに対するリーマン予想を証明した
1949年 ヴェイユ:合同ゼータ関数の一般的定式化(ヴェイユ予想)提出した
1952年 セルバーグ:セルバーグゼータ関数を発見し、リーマン予想の対応物を証明
1962年 佐藤幹夫:ラマヌジャン予想を合同ゼータ関数に対するリーマン予想(ヴェイユ予想)に帰着させた
1963年 佐藤幹夫:佐藤テイト予想を提出した
1965年 グロタンディーク:合同ゼータ関数の行列式表示を証明した[そのために一万ページに及ぶスキーム論EGA、SGAを構築]
1974年 ドリーニュ:合同ゼータ関数に対するリーマン予想(ヴェイユ予想)を証明し
1974年 レヴィンソン:リーマンゼータの虚の零点のうち少なくとも1/3(34パーセント)は実部が1/2となることを証明した
1989年 コンリー:リーマンゼータの虚の零点のうち少なくとも2/5(40パーセント)は実部が1/2となることを証明した
1995年 ワイルズ(+テイラー):フェルマー予想を証明した(楕円曲線の標準ゼータによる)
2011年 テイラー達:佐藤テイト予想を証明した(保型形式のゼータの無限系列を用いる)
20XX年 xxxx:リーマン予想解決
リーマン予想のこれまでとこれから
リーマン予想の現在地と今後の展望
リーマンが、リーマン予想を提出してから150年以上が経ちました。数学最大の難問との呼び声が高いリーマン予想は、現在までに無数の研究が行われてきました。本書は、これまでのリーマン予想の概要を振り返り、読者の方々がこれからの発展を視野に入れることができるように期待されて書かれています。

序文
リーマン(1826-1866)がゼータ関数の零点に関してリーマン予想を提出してから,今年(2009年)でちょうど150周年になる.数学最大の難問との呼び声の高いリーマン予想に関しては無数の研究が行われてきた.本書はこれまでのリーマン予想研究の概要を振り返り,これからを展望する.もちろん,これまでに行われたリーマン予想に関する研究すべてを詳細に振り返ることは本書の目的ではなく,著者による取捨選択を行っている.
本書では,第Ⅰ部において,ゼータ関数に親しむことを目的とし,有限ゼータ関数とその無限への接近を扱う,リーマン予想への導入である.この段階は,数学的には簡明なものであるが,ゼータ関数全体への展望を与えてくれる.
つぎに,第II部において,リーマン予想の研究史の概略を振り返る.リーマン予想研究が,素数の研究を推進することから進化してきたことを見て欲しい.とくに,リーマン予想のさまざまな対応物の重要性とそれらを証明するための理論や道具の整備が更なる発展を導いてきた.たとえば,有名なフェルマー予想やラマヌジャン予想もこの思想の流れで解決している.
本書の第III部はリーマン予想研究の核となる,零点の固有値解釈を中心に解説する.固有値解釈は1914年頃のヒルベルトとポリヤの提言にはじまる.これは,2つのゼータ族に対して確立されている.それは,双方とも,20世紀数学の壮大な精華である.最初に現実となったのは20世紀の前半から行われた合同ゼータのリーマン予想の研究であり,まず,1次元の場合にリーマン予想の証明が完成された(ハッセ,ヴェイユ).20世紀の後半には,その高次元の場合を証明するためにグロタンディークが空間概念を革新して1万ページに及ぶ「スキーム論」を構築し,すべての合同ゼータに対して固有値解釈を樹立した(1965年).その上でドリーニュは1974年に合同ゼータ一般のリーマン予想の証明を完成した.20世約の後半には,もう1つのゼータ族であるセルバーグ・ゼータに対しても固有値解釈とリーマン予想の証明が完成している.こちらは,リーマン多様体のゼータ関数であり,ラプラス作用素による固有値解釈が核心である.本書の特徴は,このセルバーグ・ゼータ関数をかなり詳細に解説していることである.
第IV部では,最近目覚しい発展を続けている絶対数学を取り上げる.リーマン予想の解決の観点からすると,絶対数学が光明を与えてくれるであろう.
さらに,数学研究の導入にも触れる.
読者は,本書によってリーマン予想のこれまでを知るだけでなく,これからの広大な発展を視野に入れることができるであろう.若い人達が,この未開拓の領域にはばたかれることを期待する.
2009年7月
著者
目次
序文
第I部 リーマン予想への助走
第1章 有限ゼータ関数
第2章 無限への接近
第II部 リーマン予想とその歴史
第3章 ピタゴラスからオイラーまで
第4章 リーマン
4.1 リーマンの業績
4.2 明示公式の一般化
第5章 リーマンの後
第6章 Z-カ学系のゼータ関数
−−リーマン予想の簡単な類似
6.1 やさしい事項の準備
6.1.1 線形代数からの準備
6.1.2 群論からの準備
6.1.3 微積分からの準備
6.1.4 複素関数論からの準備
6.2 Z-力学系のゼータ関数の定義
6.3 Z-力学系のゼータ関数の性質
第7章 R-カ学系のゼータ関数
第III部 リーマン予想からの発展
第8章 合同ゼータ関数
8.1 有限体
8.2 メビウス反転公式と無理数の個数
8.3 グロタンディークとドリーニュの定理
第9章 セルバーグ跡公式
9.1 フーリエ変換とフーリエ展開
9.2 ポアソンの和公式とその威力
9.3 基本群と普遍被覆空間
9.4 セルバーグ跡公式の骨格
9.5 無限次行列の場合
9.6 合同ゼータとの関連
9.7 連続無限次の場合(積分作用素)
9.8 跡公式としてのポアソン和公式
9.9 上半平面のセルバーグ跡公式
第10章 セルバーグ・ゼータ関数
10.1 セルバーグ・ゼータ関数の導出
10.2 リーマン予想が成り立つ仕組み
10.3 R-力学系のゼータとしてのセルバーグ・ゼータ関数
10.4 SL(2, Z)の跡公式とスペクトル理論入門
10.5 アイゼンシュタイン級数のフーリエ展開
10.6 スペクトルを用いた素数定理の別証
第IV部 展望
第11章 絶対数学展望
11.1 絶対ゼータ関数
11.2 黒川テンソル積の実例
第12章 研究のすすめ
12.1 数学研究とは
12.2 問題の考察の例とヒント
読書案内
[1]ゼータ関数をもっと知るために
[2]オイラーを知るために
[3]リーマン
[4]ラマヌジャン
[5]ゼータ関数の定番書
[6]絶対数学入門
[7]最近のリーマン予想の状況を知るために
あとがき
リーマン予想を解こう ~新ゼータと因数分解からのアプローチ~ (知の扉)
リーマン予想を解く練習場
リーマン予想とは、1859年にリーマンが提出してから150年以上解けておらず、数学七大問題の一つとして1億円の賞金がかけられている数学最大の難問です。本書では、リーマン予想に関する現在までの研究をわかりやすく解説し、中学生や高校生くらいの年代の人がリーマン予想を解けるように成長することを目標にしています。

巻頭図説 3分でつかむ リーマン予想が解けなかった3つの理由
リーマン予想はなぜ未解決問題なのか
(1)リーマン予想が「ゼータのわかりやすい因数分解を求めること」であることが理解されていなかった。▶︎対策:第1章
(2)ゼータの零点の練習が十分でなかった。▶︎対策:第2章、第5章、第7章、第8章
(3)解決に必要な視点の変換ができなかった。▶︎対策:第10章
今年がリーマン予想の研究開始にふさわしい3つの理由
(1)リーマン予想の研究は、1914年のハーディ論文とボーアランダウ論文で本格化した。今年はちょうど100周年。(参照▶︎第3章)
(2)絶対ゼータ・数力が準備できた。(参照▶︎第4章)
(3)ゼータの量子化・古典化がわかってきた。(参照▶︎第6章、第9章)
リーマン予想の年表

本書のスローガン
本書の読み方
本書はリーマン予想解決練習場です。
各章の関係は次の図のようになっています。

上部の空中から1章、2章、3章という第I部「リーマン予想研究」に降りて、4章、5章、6章という第II部「数力研究」に進み、7章、8章、9章、10章という第III部「ゼータ研究」に至ります。これですっかり、あなたも専門家です。リーマン予想を解いてください。
はじめに


目次
はじめに
第I部 リーマン予想研究
第1章 リーマン予想と因数分解:零点って何?
1.1 分解すること
1.2 リーマン予想
1.3 簡単なゼータ:数力
1.4 零点と因数分解
1.5 一般的なリーマン予想
第2章 リーマン予想を解析接続:零点ほしい
2.1 解析接続とは
2.2 解析接続の例
2.3 リーマンゼータの解析接続
2.4 三角数ゼータの解析接続
2.5 変化させてみよう
第3章 リーマン予想の解き方:零点をさがそう
3.1 リーマン予想の簡単な歴史
3.2 リーマン予想について知られていること
3.3 リーマン予想の解き方3通り
3.4 合同ゼータと絶対ゼータ
3.5 リーマン予想の証明法(A):絶対ゼータ・数力
3.6 リーマン予想の証明法(B):合同ゼータ
3.7 リーマン予想の証明法(C):深リーマン予想
第II部 数力研究
第4章 数力:新世紀ゼータ
4.1 数力
4.2 数力の例
4.3 関数等式の証明
4.4 a=(ω,…,ω)の場合
4.5 a=(al,a2,a3)の場合
4.6 p-数力
第5章 逆数力:反対に見たら
5.1 リーマン予想と逆関数
5.2 根を求めること
5.3 逆関数と逆写像
5.4 逆数力
第6章 古典化:絶対ゼータ
6.1 問題
6.2 問題攻略
6.3 問題の核心:古典化
6.4 解決編
6.5 発展
第II部 ゼータ研究
第7章 整数零点の規則:どんどんふやそう
7.1 問題:整数零点
7.2 問題攻略
7.3 問題設定
7.4 問題の核心:多項式版
7.5 解決編
第8章 虚の零点に挑もう:こわくない虚数
8.1 問題
8.2 問題攻略
8.3 問題の核心:オイラー積
8.4 問題解決
8.5 発展
第9章 量子化で考える:q類似
9.1 考える問題:q-完全数
9.2 問題の変形:水晶完全数
9.3 問題の核心−qを求めること−
9.4 問題の解決:どんなものも完全
第10章 逆転しよう:ひっくりかえすと楽しい
10.1 問題:逆転
10.2 問題攻略
10.3 問題の解決:L関数による表示
10.4 別の解決:オイラー数
付録 数学研究法
あとがき
索引
数学の力 高校数学で読みとくリーマン予想
高校数学からリーマン予想を紐解く
数学とは、国境を越えて存在する純粋な学問です。教育現場では重要視され、多くの人の将来の方向付けに大きな影響を与えています。本書は、「数学の持つ特別な魅力は何なのだろうか」という謎を解明するために様々な角度から数学の魅力を伝えていきます。その中でも、数学史上最大の未解決問題であるリーマン予想についてを詳しく解説していきます。

まえがき
数学には特別な力がある.数学は理工学の基礎であり現代社会を支えているとか,数学の応用によって最先端のテクノロジーが実現しているとか,そんな意味ではない.
人生において,数学という営みが人の生き方に及ぼす影響力,数学と人の精神とのかかわりの深さ,そうした観点で見たとき,数学のもつ特殊な魅力を認めざるを得ないということである.そんな事例は,数多く存在する.
四十代半ばで会社を辞め,脱サラ後の第二の人生を,数学専攻の大学院生として歩む者がいる.それはまるで,都会の喧騒を逃れ田舎に移住し農業に従事するセカンドライフにも似ている.そんな人々にとって,数学とは,大自然のようなものかもしれない.
あるいは,不登校で引きこもりだった高校生が,数学書に没頭して生きがいを見出し,独学で天才的な研究業績を上げる例もある.また逆に,数学の問題にのめり込んで他の一切に手が付かなくなり,進学や就職の機会も失い,途方に暮れる人生を送る者もいる.彼らにとって,数学とは,麻薬やギャンブルにも似た中毒性のあるものかもしれない.仮にそこまで極端なケースでなくても,定年後の趣味として緩やかに数学を楽しむ人は多いし,余暇に数学を学ぶ大人のための数学塾も盛況である.
こういう事例は,他の理工系の学問,たとえば電気工学や機械工学などでは見られないし,法学・経済学・社会学など文科系の分野でもなかなかないだろう.
しいて似た例を探すとすれば,文学や音楽などの芸術系の営みに,共通点があるかもしれない,趣味とする人々がいる一方,プロを目指しそれに没入して人生を棒に振る人々が少なからず,それも国境を越えて世界の至るところに存在する点など,確かに似ている.そういう意味ではスポーツとも共通点がある.数学者として身を立てることは,プロのスポーツ選手になるくらいに厳しい道のりであり,狭き門であるという見方もできる.
芸術やスポーツの世界で日本人の若者が世界的に活躍してニュースになると,テレビなどマスコミがその人の生い立ちから世界デビューまでの道のりを紹介することがある.かつて,私の妻がそうした報道を見て「数学者が世に出る経緯にそっくりね」と言ったことがある.確かに,無名時代の苦労から,収入に結びつかない努力をしながらの下積み,そして,海外に単身で乗り込み世界の最先端を学び,業績を上げて帰国した後は,世の中から手のひらを返したように評価される様は,少なからず共通している.
実際,海外生活の中身にも共通点は多い.もし,仕事の内容を見ずに生活スタイルや人とのかかわり方だけを追えば,数学者の暮らしぶりは,芸術家やスポーツ選手と区別がつかないだろう.
しかし,数学は決して,美術でも音楽でもスポーツでもない.純粋な学問,それも理系の基礎をなし歴史と伝統の最たる学問である.そのうえ,中学高校の教育では主役を張り,大学入試でも重視され,たくさんの人々の生涯の方向付けに大きな役割を演じている.こんな学問は他にないだろう,なぜ,数学にはこんな力があるのだろう.数学がもつ特別な魅力とは,いったい何なのだろう.
本書は,その謎を解明するための試みの一つである.攻略は,決して容易ではなく,そもそも一言で答えが述べられるようなものではないだろうが,本書では,いろいろな角度から例を挙げて数学の魅力を伝えてみたい.
そして,その中でも究極の題材が,数学史上最大の未解決問題であるリーマン予想である.本書は,リーマン予想がどんな問題なのか,高校数学を前提として解説する.それによって,数学の魅力の一端を伝えていければと思っている.なお,高校数学に属さない事項を補うため,巻末に付録を付けて解説した.本文だけを通読して一通りの理解ができるように努めたが,数学的な厳密さが気になる読者は,付録を使って勉強できるようになっている.
奥深い数学の世界を,本書を通じて一緒に探求して頂ければ幸いである.
著者
数学の力
高校数学で読みとくリーマン予想
目次
まえがき
第1章 数学の力とは
1.1 数学研究とは~簡単な例を通して
1.2 素数が無数に存在すること
1.3 第一の力
1.4 何がうれしいか
1.5 第二の力
1.6 足し算と掛け算
1.7 ABC予想
1.8 平方数の和となる素数
1.9 バーゼル問題
第2章 リーマン予想と素数
2.1 ユークリッドからオイラーへ
2.2 大きな無限大
2.3 素数の逆数の和
2.4 ゼータ関数
2.5 複素平面
2.6 解析接続
2.7 関数等式
2.8 複素積分
2.9 素数定理
2.10 リーマン予想と素数
第3章 深リーマン予想
3.1 平方数の和となる素数(再考)
3.2 深リーマン予想とは
3.3 オイラー積の収束とは
3.4 深リーマン予想と素数
3.5 ディリクレ指標
3.6 算術級数定理
3.7 数値計算による検証
(A) L(s,x3)
(B) L(s,x4)
(C) L(s,x5a)
(D) L(s,x5b)
(E) L(s,x6)
(F) L(s,x7a)
(G) L(s,x7b)
(H) L(s,x7c)
(I) L(s,x8a)
(J) L(s,x8b)
付録A 環論と合同式
A.1 環論の基礎
A.2 合同式の解法
付録B テイラー展開
B.1 基本的な考え方
B.2 収束半径
B.3 テイラーの定理
付録C アーベルの総和法
C.1 基本的な考え方
C.2 部分和の公式
C.3 応用例
あとがき
索引
リーマン予想は解決するのか? ―絶対数学の戦略―
ことばでイメージするリーマン予想
本書は、150年以上も数学者たちが挑み続けている数学の難問である「リーマン予想」、また、その解決に最も近いとされている戦略である「F1スキーム」とはどのようなものなのかを紹介しています。難解な数学でも数式を使わず言葉によるイメージで理解できるように工夫しているため、数学が苦手な人でも楽しむことができます。

リーマン予想は解決するのか? 目次
本書の読みかた 小島寬之
I
現代数論の戦略 〈数〉の過去・未来 2008.09.29
素数の歴史…現代数論の戦略…オイラーの作法…リーマン予想の解法とその影響…ラマヌ ジャンの業績と特異性
絶対数学の戦略 リーマン予想のXデー 2009.02.27
リーマン予想とはなにか? のおさらい…リーマンはなぜリーマン予想に行き着いたのか…素数定理…ゼータ関数とリーマン予想…ゼータ関数の歴史遍歴…p進数の世界…F1とスキームの最前線…F1からリーマン予想へ…スキーム論の考え方…F1理論とカテゴリー、そして未来
☆
リーマン予想まであと10歩 小島寛之 2009.04
10歩手前 数の宝石(素数)…9歩手前 無限に足しても有限(数列の収束)…8歩手前 神秘の関数(ゼータ関数)…7歩手前 空想の理想郷(複素数)…6歩手前 象のしっぽを触って全体を知る(解析接続)…5歩手前 複素数世界で整数をリニューアルする(ガウス整数とガウス素数)…4歩手前 集合を「数」に見なしてしまう技術(イデアル理論)…3歩手前 すきまのない数世界(実数とP進数)…2歩手前 全素数に関する積と全自然数に関する和の一致(オイラー積)…1歩手前 ゼータの値がゼロになる場所(リーマン予想)
II
ゼータへの旅 黒川信重 2006.06
1 素数空間 2 素数の演劇空間 3 空間とは 4 空間のゼータ 5 軌跡空間 6 ゼータの表わす未知空間
絶対数学 黒川信重 2000.09
1 二〇世紀は環の世紀 2 微分 3 二〇世紀の数学の欠陥と二一世紀数学の展望 4 絶対数学 5 ゼータ 6 絶対空間とモナド 7 クロトーネの海辺にて
付録 絶対数論研究集会報告――リーマン予想最後の一歩へ 黒川信重
本書の読みかた
本書は、現在最も解決が待望される数学の難問「リーマン予想」とは何かを指南し、その上で現在最前線の数学者たちが押し進め、解決に最も至近距離にあると思われる攻略のための戦略、「F1スキーム」、を紹介するエキサイテングな本です。しかも、非常に難解な数学について、数式をほとんど使わず、ことばによるイメージによって、美味しいところだけをご賞味いただけるように工夫してあります。
そんなわけで本書は、「高校生レベルから読めるけど、プロ級の人が読んでもスリリングな本」に仕上がりました。具体的には、熱気溢れる対談(I章)と初級解説(☆章)と本格派解説(II章)の三部から構成されています。
もちろんどのように読み進めていただいても構いませんが、どう読んで行こうか迷われたり、途中で知らない用語にぶつかって焦ったりされた場合には、以下を道案内としてご利用ください。きっと楽しみ方の幅が広がること請け合いです。
1 数学のホットな最前線を知りたい方
→I章から読み始め、分からない用語で困ったら、☆章に解説があるか探して、あったら寄 り道して、また戻る。
2 十分な予備知識を持ってから、最前線に挑みたい方
→☆章を読んでウォーミングアップしてから、I章、そしてII章へ。
3 時間軸を追って(あるいは最新の知見をとにかく真っ先に)読みたい方
→目次の日付を参照してください。
4 まずはプロの数学者のお手並み拝見、という方
→IIから入り、I、☆とお進めください。
では、わくわくどきどきの数学新世界でお待ちしています。
ナビゲーター・小島寛之
リーマン予想とはなにか 全ての素数を表す式は可能か (ブルーバックス)
全ての素数が完全にわかる
「リーマン予想」は150年前に生まれた数学の未解決問題で、難解にもかかわらず人気があります。本書では、リーマン予想の全体像と意味について丁寧に解説されています。数学の奥深さがわかる1冊です。

はじめに
数学は、同じ自然科学の中でも、物理学や化学とは大きく異なる点があります。その一つは、画期的な業績を上げても、それで大金を手にするようなことは基本的にないだろうということです。しかし、中には例外もあります。その一つが、本書のテーマである「リーマン予想」の解決です。成功すると、少なくとも100万ドルを手にすることができます。もちろんそのような大金を提供しようとする人がいるわけは、リーマン予想の解決が、私たちがこの世界を理解するうえで、とても大きな進展をもたらすだろうと期待されているからです。
リーマン予想というのは、今から150年ほど前に生まれた数学の問題です。問題文としては今でも、当時と変わっていません。150年間何も変わっていないのなら、この間数学者は怠けていたのでしょうか?もちろんそんなことはありません。多くの数学者が、血のにじむような努力を重ねてきました。関連する研究の成果は、数学の世界を大きく変えてきています。それでも、いまだ解かれていない難問なのです。
ところで、リーマン予想とはどのような問題でしょうか。
それは、「リーマンのゼータ関数と呼ばれる複素数の関数の値が、どのような場合に0(零)になるか」という問題です。リーマンは、このような場所がどこであるかを予想したのですが、彼自身はそのことを証明することはできませんでした。そこで、後世にそれが正しければ証明し、間違いであれば反例を示すことが問題として残ったのです。
しかし、ある関数の性質が、どうしてそこまで重要な問題になるのでしょうか。
実は、リーマンのゼータ関数がどのような場合に0になるかを完全に知ることによって、原理的には全ての素数を知ることができるようになるのです。素数は、古代ギリシャの昔から、人々の興味を惹いてきました。それでも疑問は次々にわいてきます。素数の全てを知ることができれば、これまでにわからなかった素数に関する多くの事柄がわかることになります。また、素数にまつわる新たな発見ももたらされるでしょう。そのような期待があるからこそ、ここまでリーマン予想が注目されるのです。
注目の高さの反映として、リーマン予想をテーマにした書物はたくさん出版されています。しかし、リーマン予想と素数を結びつける、リーマンの研究の数学的な詳しいことについては、専門書を読むしかないでしょう。そこで、本書は、その点に、少しだけ踏み込んでみます。でも、専門書では読者がもっていると仮定されている数学的な知識も、できるだけ説明するようにします。ただし、専門書に比べるとどうしても少しざっくりとした説明になることをご容赦ください。
本書では、第1章で、リーマン予想と素数の結びつきについてのあらすじを説明します。数学的な詳しいことにあまり興味がない、あるいは理解する自信がないという人でも、この章は頑張って読んでみてください。その後の第2章から第5章は、数学的なことを少し踏み込んで知りたい人のために、第1章の説明のうち、ポイントとなる部分について説明していきます。とはいえ、あまり専門的にならないようにします。また、少し込み入った数式の操作が必要な事柄については、付録にまとめます。最後の第6章では、リーマン予想が生まれた後の研究の進展についてまとめます。
したがって、とにかく全体像を知りたいという人は、第1章に続けて第6章を読めば、十分だと思います。
リーマン予想が、いまだ解かれていないのは、究極まで考え抜かれた問題だったからなのです。このことは、この問題を考え出したリーマンが、大変に優れた数学者だったことを物語っています。実際、現代数学の基礎は、彼によって築かれたといっても過言ではありません。本書では、リーマンが現代の数学の基礎に広くかかわっていることもわかるように工夫してみました。
この本が、リーマン予想について、読者がこれまでより深く理解する助けになることを願っています。
平成27年8月 中村 亨
もくじ
はじめに
第1章 リーマン予想とは何だろう
1.1 素数の分布
素数とは
100以下の素数
素数はどこまでも増え続ける
双子素数予想
グリーン-タオの定理
素数の間隔はいくらでも大きくなる
素数の個数を表す関数π(x)
π(x)がわかることと全ての素数がわかることは同じ
π(x)の振る舞い−100まで
π(x)の振る舞い−1000まで
素数定理
リーマンの研究の目的
1.2 リーマンのゼータ関数 –
バーゼル問題とゼータ関数の出現
オイラー積表示
π(x)とゼータ関数
リーマンのプログラム
複素数の登場
リーマンと複素関数
リーマンのゼータ関数に関する研究
関数等式とリーマン予想
ゼータ関数のさらなる追求
リーマンのプログラムの完成
第2章 オイラー積とは
2.1 ゼータ関数
無限和の表し方
ディリクレの関数
nsとは何だろう
指数関数
自然対数
積の対数は、対数の和
自然対数の底
結局、nsとは
2.2 オイラー積
不思議な因数分解
約数となる素数が2だけの数の逆数を全部足す
約数となる素数が2か3だけの数の逆数を全部足す
オイラー積登場!
オイラー積の正しい説明
第3章 リーマンのゼータ関数とは
3.1 複素関数とは
複素数の四則演算
代数学の基本定理
複素平面
3.2 リーマンのゼータ関数
ゼータ関数の成分①:指数関数ez
ゼータ関数の成分②:Γ(S)
ゼータ関数の成分③:複素関数の積分
複素数の極形式と対数
複素関数の積分とは
コーシーの定理
複素微分とは
ゼータ関数は正則か
コーシー-リーマンの方程式
ゼータ関数は一つだ!
第4章 リーマン予想とは
4.1 リーマンのゼータ関数の極
ゼータ関数の特異点
(e2πis-1)=0となる時
正則関数のテイラー展開
零点での関数の形
Γ(s)=0となる時
複素関数のローラン展開
極での関数の形
留数と留数の定理
ここまでのまとめ
ゼータ関数の極はs=1だけ
4.2 ゼータ関数の零点
ゼータ関数の関数等式
ゼータ関数の零点
リーマン予想の誕生
臨界線とζ(s)の対称性
第4章のまとめ
第5章 リーマンの素数公式とは
5.1 ゼータ関数の積表示
グザイ関数ξ(s)を作る
ξ(s)の極
ξ(s)の零点
(5.2)式のからくり
多項式の積表示
オイラーの研究
ゼータ関数の非自明な零点の分布
5.2 素数公式
J(x)をζ(s)から計算する
対数積分Li(x)
後ろの2項は定数とみなせる
π(x)をJ(x)から計算する
π(x)の計算
リーマンの素数公式
その後
第6章 それから
素数定理のその後
零点の計算
鏡像の原理
近似計算
臨界線上の零点の存在
ジーゲルの発見
非自明な零点探索の加速
ゼータ関数の研究のその後
付録1 オイラー積とJ(x)
付録1.1 オイラー積からJ(x)の(付1.2)式を求める
付録1.2 関数J(x)とπ(x)
付録2 J(x)の方程式を解く
付録2.1 フーリエ変換とリーマン
付録2.2 リーマン積分
付録2.3 J(x)の方程式を解く
付録3 ゼータの特殊値
付録4 数式のまとめ
参考になる本
さくいん





















