ページコンテンツ
【最新 – リーマン予想を知る・学ぶおすすめ本 – いつ証明されるのか?】も確認する
リーマン予想を視覚で理解する
「リーマン予想」とは、約1億円の賞金がかけられている数学界で最大の難問です。この予想で用いられる「ゼータ関数」は、「素数」と密接に関係しています。本書は、ビジュアルにこだわり視覚化したうえで、ゼータ関数と素数との関係を理解できるように解説しています。

はじめに
本書の目標
本書は,2016年に行った社会人,高校生・大学生向けセミナー「素数の世界~世紀の難問「リーマン予想とは!?」」(和から株式会社主催)の講義録を大幅に改訂したものです.私は,このセミナーの講師として,1回3時間全6回にわたり,数学を専門としない社会人・学生向けに,できるだけ分かりやすく数学の本質を見失わない程度に平易にしたうえでリーマン予想の解説を行いました.
「リーマン予想」とは,賞金100万ドル(約1億円)の懸賞金がかけられている数学界で最大の謎の一つです.ゼータ関数の零点に関する予想ですが,驚くべきことにこの「ゼータ関数」は,「素数」と密接に関係しているのです.同セミナーは,おかげさまでたくさんの方から応募があり好評をいただきました.一見素数とは何の関係もないように思われる「ゼータ関数」と「素数」が密接に関係しているということに,多くの方が「ロマン」を感じたのだと思います.私は当時もっていた知識を総動員して「ゼータ関数」と「素数」との関係を説明しましたが,セミナーが終了した後も,もっと分かりやすく「ゼータ関数」と「素数」との関係を説明できたらよいのにと常々思っていました.
本書の最終目標は,できるだけたくさんのグラフや図を利用して,この「ゼータ関数と素数との関係」を理解することにあります.この「素数」と「ゼータ関数(より正確にはゼータ関数の零点)」にはコインの「表」と「裏」のような関係があります.例えば,数が大きくなればなるほど素数の個数(出現割合)は減っていきますが,逆に,ゼータ関数の零点(零点の中でも非自明零点と言われるもの)は,数が大きくなればなるほど増えていきます.また,素数から得点を生成することも,逆に,零点から素数を生成することもできます.
本書の目標は,同セミナーでは十分に説明しきれなかった内容を含めて,ビジュアルに視覚化したうえで,この「素数とゼータ関数の零点との関係」を理解することにあります.
まずは,今後の見通しをよくするために,「素数」と「ゼータ関数」の関係をざっと見ていきましょう.この「はじめに」では,「ゼータ関数」や「零点」などの用語を詳しい説明をせずに使用していますが,詳細は後に説明しますので,ここでは分からなくても気にせず,「素数」と「ゼータ関数」の関係をざっと眺めてみてください.
素数
素数とは,2,3,5,7,11,13….など,1とその数以外に約数をもたない自然数です.Figure 1は,素数の位置に黒線を引いて素数の分布を表したものです.例えば,Figure 1(a)は,左端を1,右端を1000とし,一番左の黒線が2を,一番右側の黒線は997(1000以下の最大の素数)を表しています.1から1000までには素数が168個ありますので,168本の黒線が描かれています.バーコードみたいですね,名付けて「素数バーコード」です.同様に,(b)は1001から2000まで,(c)は100万1から100万1000まで,(d)は10億1から10億1000まで,(e)は1兆1から1兆1000までにある素数を黒線で表したものです.
これらを見ると,素数が現れる割合はどんどん減っていることが分かります.Table 1は,それぞれの開始数から1000個の自然数の中に何個の素数が含まれているか示したものです.素数の出現割合は減っていることが分かりますが,一方で「開始」が3桁(1000倍)増えているのに比べると,素数の出現割合はそれほど減っていないと捉えることもできます.「開始数」を1000倍したからといって,その周辺にある素数の数が1000分の1になるわけではないのです.このように,素数の出現割合は減っていくものの,その減り方はゆっくりなのです.この素数の出現割合がどのように減っていくのか表しているのが素数定理です.素数定理については,Part Iで詳しく見ていきます.
素数バーコードから分かることはこれだけではありません.素数バーコードを見ると,素数は満遍なく出現するのではなく,ところどころ偏りながら出現することも分かります,素数がしばらく現れない部分があるかと思えば,連続して素数が現れる部分もあります.この素数が現れる場所のことを素数の分布と言います.素数の分布を調べることとは,素数パーコードにおいて,黒線がどのような場所に現れるのか,また,どのような法則で現れるのかを研究することです.本書の最終目標は,この素数の分布がゼータ関数の零点でどのように表されるのか理解することにあります.
Table 1:自然数1000個当たりに含まれる素数の数と割合
| 開始数 | 素数の数 | 素数の割合 |
| 1 | 168 | 0.168 |
| 1,001 | 1351 | 0.135 |
| 1,000,001 | 75 | 0.075 |
| 1,000,000,001 | 49 | 0.049 |
| 1,000,000,000,001 | 37 | 0.037 |

ゼータ関数

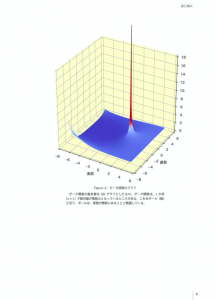
Figure 2:ゼータ関数のグラフ
ゼータ関数の零点一自明な零点一

Figure 3: ゼータ関数の負のグラフ
ゼータ関数の零点−非自明な零点−
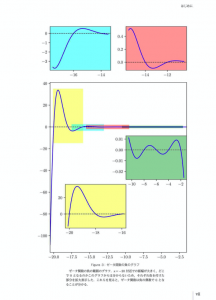
ここまで,ゼータ関数のポールと自明な零点が素数の分布と関係があることをざっと見てきましたが,ゼータ関数には自明な零点の他に,もう一つの重要な得点の集まりがあります. Figure 4は,ゼータ関数の値(複素数)を偏角で色分けしたものです(偏角についてはPart III参照).このグラフからゼータ関数の零点を見つけていきましょう.上の図(a)は複素数の偏角を色分けしたカラーサンプルです.複素平面上で偏角が0(つまり実軸の正の方向)の付近は赤,半時計回りに黄色→緑となり,偏角が180度(つまり実軸の負の方向)では水色となって青→紫→赤に戻ってくることが分かります.原点は,赤・緑・青が接していることを覚えておきましょう.
下の図は,ゼータ関数の値の偏角をカラーで表したものです.右半平面(つまり,実部が正の範囲)上では赤一色になっています.これは,この範囲でゼータ関数の偏角が0付近にあることを示しています.また,負の実軸上では周期的に色が変わっているところがありますが,これが,先ほど見た自明な零点です.カラーマップで見たとおり赤・緑・青が接しているところが零点であり,例えばs= -2で赤・緑・青が接していることが分かります.同様に,負の偶数では赤・緑・青が接していることを確認できます,s=-2からs=-10までに赤・緑・青が接している部分が5個あることを確認してみましょう.
■非自明点
ゼータ関数の零点のうち,自明な零点以外を非自明な零点と言います.
Figure 4の下図では,赤・緑・青が接しているところがy軸上(つまり虚軸上)の付近にあることが分かります.例えば,虚軸の14の付近(つまり14i付近)に赤・緑・青が接しているところがあります.この点をよく見ると,虚軸からわずかに右側にずれていることが分かるでしょうか※2.21i,25i付近の虚軸からわずかに右側に外れたところにも,赤・緑・青が接している点があり,実は,ここにもゼータ関数の零点があるのです.これらが,ゼータ関数の非自明零点です.非自明零点については,Part VIIで確認します.
■リーマン予想
カラーマップを見ると,非自明零点は実軸からわずかに右側にずれた縦一直線にならんでいるように見えます.この縦の直線のことをクリティカルラインと言います.そして,本書のテーマであるリーマン予想とは,すべての非自明零点がクリティカルライン上にあるという予想です.コンピュータを使うことにより1兆個を超える非自明零点の位置が計算されていますが,現在までに判明している非自明零点はすべてクリティカルライン上にあります.つまり,現在までに判明している非自明零点は,すべてリーマン予想を満たしているのです.しかし,未だこの証明には誰も成功していません,リーマン予想についてはPart VIIで確認します.
※2 原点の右横にある赤・緑・青が接している部分は,点ではなくポールです.
Figure 4:ゼータ関数の偏角のカラーマッピング

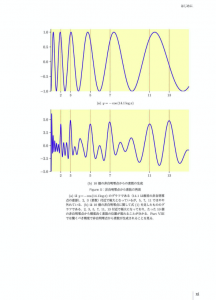
非自明零点から素数を作る

Figure 5:非自明零点から素数の再現
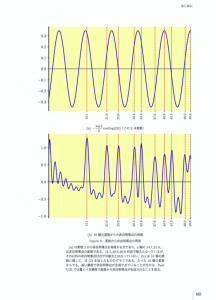
素数から非自明零点を作る

Figure 6:素数から非自明点の再現
素数とゼータ関数のまとめ
ここまでお話ししてきた「ゼータ関数」と「素数」との関係はTable 2のとおりです.
ゼータ関数には,「ポール」と「零点」があり,「零点」には「自明な零点」と「非自明な零点」があります.このそれぞれが,素数との間で関係があるのです.
Table 2:ゼータ関数のポール・寄点と素との関係

Figure 7: ゼータ関数のボールと書点の位置
Contents 目次
はじめに
Part I 素数の不思議な性質
第1章 素数の性質
1.1 素因数分解の一意性
1.2 素数が無限にあること
第2章 素数を数えよう
2.1素数を数える関数−素数計数関数π(x)−
2.2 素数計数関数の形状
2.3 素数定理入門
2.4 素数定理を精緻化する
Part II ゼータ関数
第3章 ゼータ関数登場
3.1 ゼータ関数
3.2 調和級数
3.3 調和級数による素数の無限性の証明
第4章 バーゼル問題 −ζ(2)の値−
4.1 バーゼル問題
4.2 sinxのテイラー展開
4.3 sinxの無限乗積展開
4.4 バーゼル問題を解く
4.5 ゼータ関数の正の偶数での値
4.6 ウォリスの公式
Part III imaginaryな世界へようこそ
第5章 複素数乗とは
5.1 定義域を複素数へ拡張する
5.2 複素平面
5.3 オイラーの公式
5.4 正の数の複素数乗
5.5 複素数の複素数乗
5.6 ゼータ関数の定義域を複素数へ拡張する
5.7 ゼータ関数の微分
第6章 正則関数の零点とポール
6.1 零点とポール(極)はなぜ重要か
6.2 正則関数の零点
6.3 正則関数のポール(極)
6.4 除去可能特異点
6.5 ローラン展開と留数
6.6 留数
6.7 留数定理
第7章 解析接続とは
7.1 ゼータ関数の定義域
7.2 関数の姿
7.3 解析接続とは
Part IV ゼータの兄弟−ガンマ関数−
第8章 ガンマ関数
8.1 階乗関数
8.2 ガンマ関数の定義
8.3 ガンマ関数の漸化式
8.4 ガンマ関数を解析接続する
第9章 ガンマ関数の性質
9.1 ガンマ関数の零点とポール
9.2 ガンマ関数の基本公式
Part V 1+2+3+…=-1/12
第10章 ゼータ関数の解析接続
10.1 一般二項定理
10.2 ゼータ関数の新化式
10.3 ゼータ関数の解析接続
第11章 ゼータ関数の整数での値−特殊値−
11.1 ゼータ関数のポール
11.2 Res<1における漸化式の簡易化
11.3 ζ(0)とζ(-1)を求める
11.4 ゼータ関数の解析接続−負の整数−
11.5 ベルヌーイ数とは
11.6 ゼータ関数の負の整数をベルヌーイ数で表す
第12章 オイラー,ラマヌジャンによる不思議な方法
12.1 1+2+3+4+…=-1/12?
12.2 オイラー,ラマヌジャンによる方法
12.3 片側極限
12.4 アーベル総和法
12.5 イータ関数
12.6 オイラー,ラマヌジャンの方法の正当化
12.7 ζ(0)を求める
Part VI 太陽と月の美しい関係
第13章 un beau rapport−オイラーによる美しい関係−
13.1 Beautiful Relation
13.2 オイラーによる関数等式
13.3 リーマンによる関数等式
第14章 関数等式の証明
14.1 ガンマ関数とゼータ関数の関係
14.2 関数等式(非対称型)から関数等式(対称型)の導出
14.3 関数等式の証明―積分を計算する―
14.4 関数等式の証明―もう一つの積分計算―
14.5 関数等式の証明―留数定理を用いる―
14.6 正の偶数における特殊値
Part VII リーマン予想
第15章 ゼータ関数の零点とリーマン予想
15.1 関数等式の意味
15.2 ゼータ関数の零点
15.3 リーマン予想
15.4 非自明零点の分布
第16章 リーマン予想と同値な命題
16.1 素数定理との関係
16.2 メビウス関数とメルテンス関数
16.3 メルテンス予想とリーマン予想
16.4 ファレイ数列
16.5 ファレイ数列とリーマン予想
Part VIII 素数で輝く
第17章 素数階段を表す
17.1 ゼータ関数と素数との関係
17.2 マンゴルト関数とチェピシェフ関数
17.3 ディリクレ級数と階段関数の関係―ペロンの公式―
17.4 ψ^xの積分表示
17.5 ψ^x(x)の明示公式
17.6 マンゴルト明示公式の意味―近似項―
第18章 素数定理
18.1 素数定理を用いて言い換える
18.2 補題18.1.1の証明
18.3 素数定理の証明のアイデア
18.4 Res=1上に零点がないこと
第19章 素数で輝く
19.1 リーマンスペクトル
19.2 マンゴルト明示公式の意味―周期項―
19.3 マンゴルトの明示公式のグラフ1
19.4 マンゴルトの明示公式のグラフ2
19.5 周期項を微分する
19.6 素数で輝く
19.7 リーマンスペクトルで輝く













